🔷 시작하며, 흐름 정리
지난 포스팅에서 우리는 n-gram Language Model에 대해서 알아보았다. 이번 글에서 알아볼 것은 n-gram Language Model이 가지고 있는 치명적인 단점을 극복시켜줄 Neural Language Model이다.
n-gram Language Model의 문제점부터 복습해보자. n-gram Language Model은 앞의 n-1개의 단어만을 보고 n번째 단어를 예측한다. 예를 들어 "students opened their"이 1000번 나왔고, "students opened their exams"가 100번 나왔다면, "students opened their" 다음에 "exams"가 나올 확률은 0.1(100/1000)이다. 따라서 n이 커질 수록 그 특정 단어 시퀀스가 등장하지 않을 가능성이 높다. 이로 인해 Sparsity 문제가 커진다. 두 번째로 확률을 통계기반으로 낸다. count를 저장해야하기 때문에 저장공간(Storage problem)이 더 많이 필요하게 된다.
🔷 Neural Language Model

지금까지 우리가 배운 모델들은 중심 단어를 기준으로 앞뒤로 고정된 window size만큼의 단어를 본다. window size 밖의 단어는 고려하지 않는다. 워드 임베딩 벡터들을 합처 벡터 e를 생성하고, 벡터 e는 hidden layer에 입력하여 나온 결과 h를 softmax 함수에 넣어 확률 분포가 결과로 나온다. 이처럼 특정 개수의 단어를 neural network의 input으로 받는 모델을 Fixed-window Neural Network LM이라고 한다.

이 방법은 기존의 n-gram이 가졌던 문제점을 두 가지를 해결한다. fixed-window neural LM은 통계 기반이 아니라 워드 임베딩을 활용하므로 Sparsity 문제가 해결된다. 또 n-gram을 저장할 필요가 없으므로 Storage 문제도 해결된다.
하지만 여전히 남아 있는 문제가 있다.
• 고정된 window 사이즈가 너무 작다. -> 문맥을 반영하지 못한다.
• window 사이즈가 커지면 W도 커진다.
• Symmetry 하지 않다(=대칭성이 없다). 같은 단어일지라도 단어의 위치에 따라서 곱해지는 가중치가 다르기 때문이다. 따라서 비슷한 단어를 학습해도 새로 다시 학습해야 한다.
🔷 Recurrent Neural Networks (RNN, 순환신경망)
위의 문제점을 해결하기 위해 RNN이 등장한다. RNN의 핵심 아이디어는 똑같은 W를 계속하여 곱한다는 것이다. 단어가 같으면 자리에 상관없이 같은 결과가 나올 것이다. Symmetry해진다.
단어가 입력되면 임베딩 벡터 e(t)를 추출한다. e와 W를 곱한 값을 이용해 h를 구한다. h는 softmax함수에 입력되어 확률 분포 결과를 낸다.

기존에는 W의 행 개수에 따라 input의 개수가 정해졌었다. 그런데 RNN은 W가 같기 때문에 input의 개수가 정해져 있지 않다. 또 워드 임베딩 벡터를 똑같은 W에 곱하기 때문에 Symmetry하다. 이전 값의 영향도 받았으므로 순서도 고려된다.

위 자료의 내용을 정리해보자
장점
• 어떤 길이든 input으로 줄 수 있다.
• 이론적으로 time step t에서 이전 단계의 정보를 사용할 수 있다.
• input이 커진다고 해서 모델이 커지지 않는다. (Wh 와 We만 있으면 됨)
• symmetry하다.
단점
• 순차적으로 계산되어야 하기 때문에 느리다
• 먼 곳의 정보를 잘 반영하지 못하는 경우도 있다. (이론적으로는 잘 되어야 하지만)
🔷 RNN 언어 모델 학습
어떻게 학습시켜주면 될까?
단어들의 집합이 담긴 큰 corpus를 가져온다.
이를 RNN-LM에 입력하고 매 step마다 ŷ(t)를 계산한다.
step t에 대한 loss function에 cross entropy 연산을 한다. 정답값과 ŷ(t)를 비교해주는 것이다.

그리고 전체 training set에 대한 전체 손실을 구하기 위해 평균을 구한다.

RNN LM은 Teacher Forcing 방식으로 학습한다. Techer forcing을 간단히 말하면 모델이 예측한 값이 아닌 실제 정답값을 강제로 넣어주는 것이다. 연속적인 예측을 수행할 때 한 time step에서 잘못 예측하면 계속해서 잘못된 추론이 입력으로 들어가게 된다. 따라서 각각의 입력값은 정답값으로

전체 큰 그림은 이렇게 된다.
🔷 RNN 매개 변수 학습
가중치는 Backprogation을 통해 업데이트 해준다. (간단히 패스,.. 이에 관해서는 나중에 업데이트 하겠음)
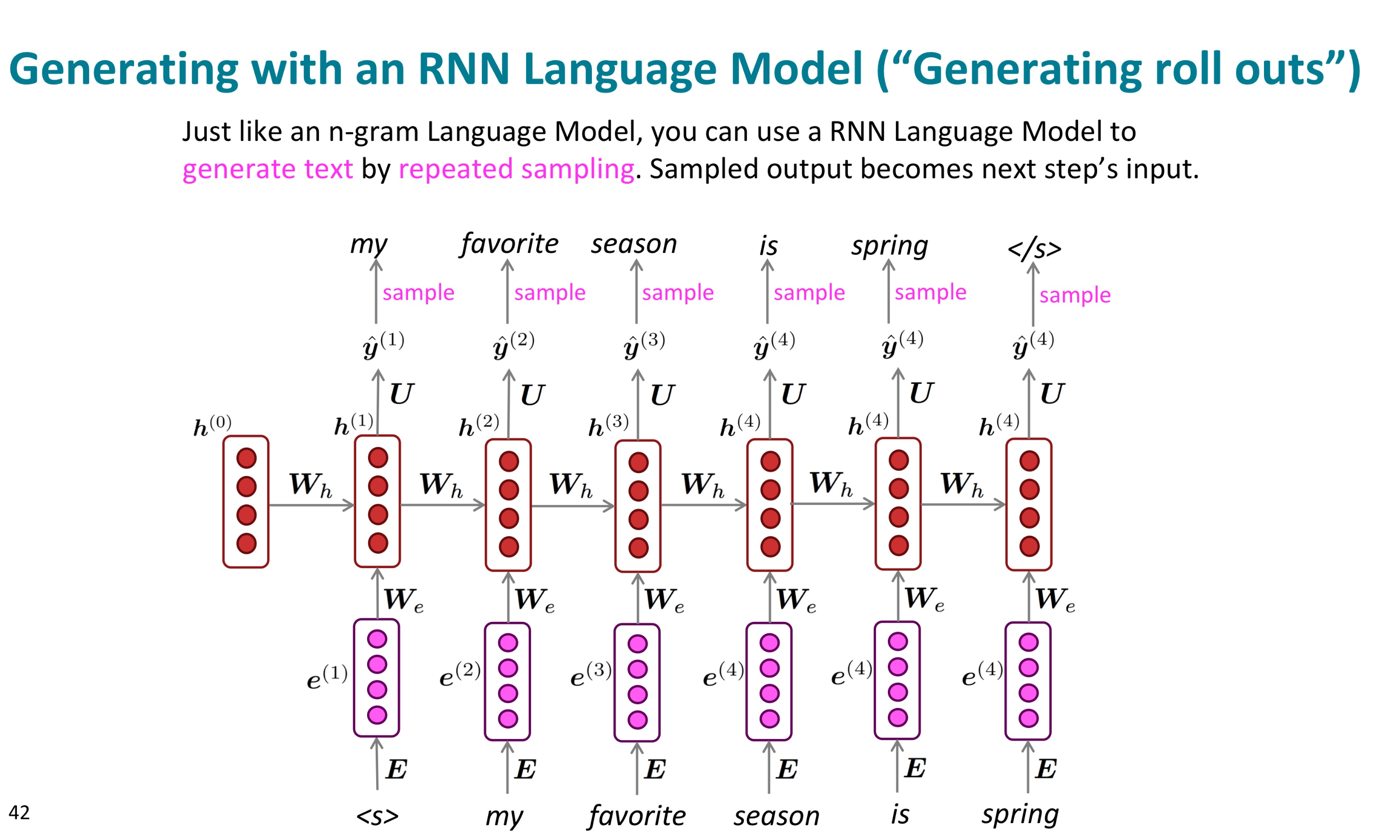
그래서 이렇게 다음 토큰을 생성하는 RNN을 언어 모델으로 사용할 수 있다.
🔷 Perplexity
이렇게 학습한 모델의 성능은 어떻게 평가할까? Perplexity 라는 평가 척도를 활용한다. perplexity란 영어로 당황, 혼란을 의미한다. 그래서 여기서는 애매함의 정도라고 생각하면 된다. 그래서 낮을 수록 성능이 좋다는 것을 의미한다. 식은 아래와 같다.
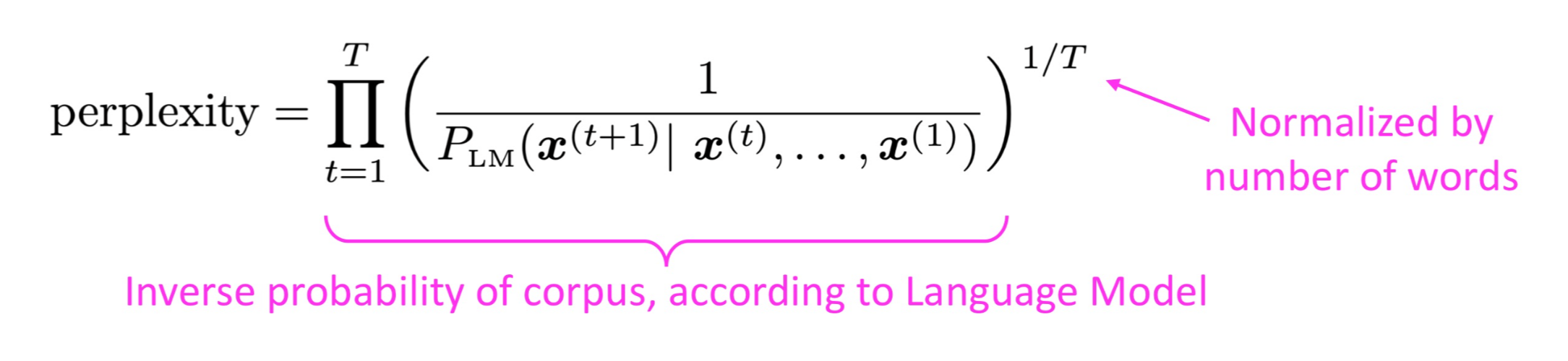
어떤 토큰이 들어왔을 때 생성한 다음 토큰에 대한 정확도의 역수이다.
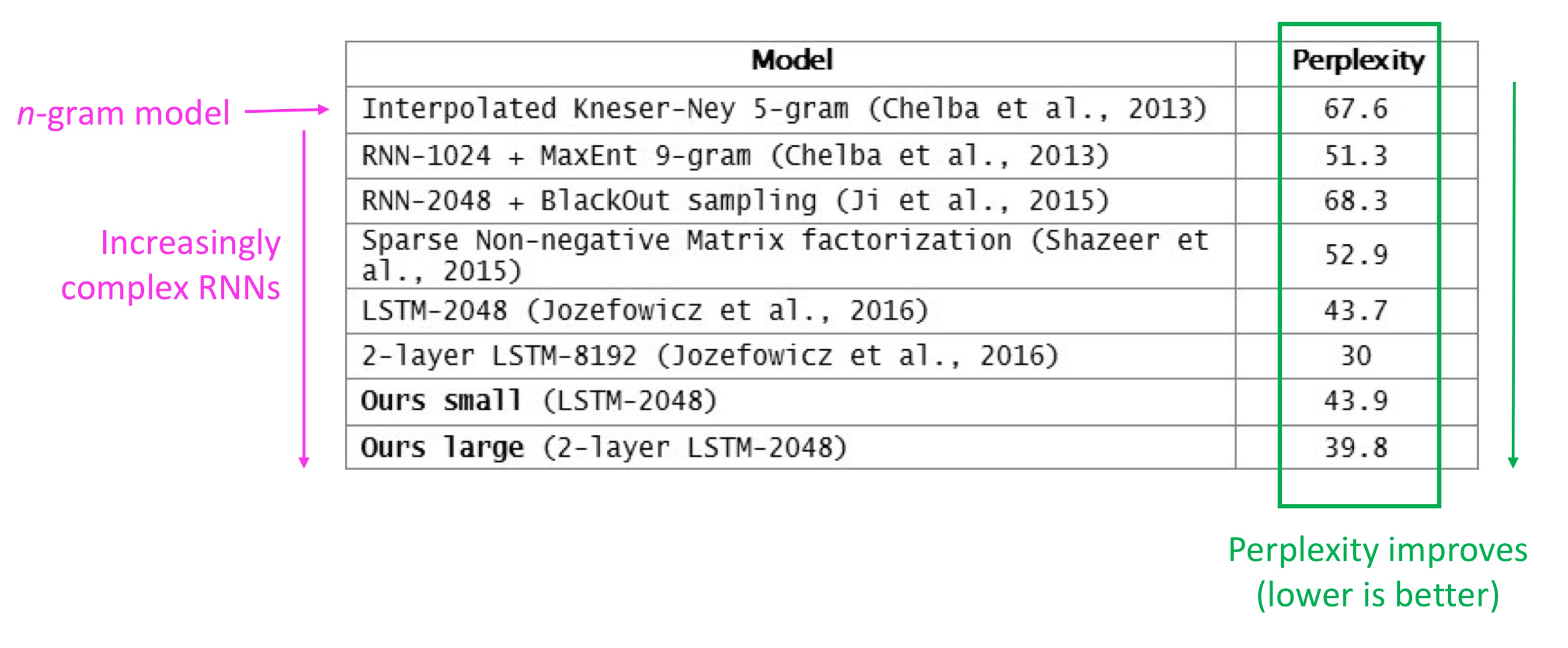
다음 사진은 모델들을 perplexity로 평가한 결과이다. 하지만 perplexity가 낮다는 것은 테스트 데이터 상에서 높은 정확도를 보인다는 것이지, 사람이 느끼기에 좋은 언어 모델이라는 것을 반드시 의미하진 않는다고 한다. 그래서 요즘 모델들을 평가하기에는 부적합하다고 한다.
🔷 RNN의 문제점: Vanishing gradient problem
RNN에서는 backpropagation 과정에서 chain rule을 이용해 미분값을 구한다. 이때 작은 값들끼리 계속 곱해지기 때문에 미분값은 계속해서 작아지게 된다. 이는 멀리 있는 단어의 dependency에 약하다는 문제점이 된다. 예를 들어
"내가 티켓을 프린트하려고 했는데 프린터기에 토너가 없다는 것을 알았다. 나는 주변 마트에 가서 토너를 샀다. 좀 비쌌다. 토너를 프린터에 설치한 다음에서야 나는 프린트를 했고 결국 인쇄된 _____ ... "
이런 문장이 있을 때, RNN-LM은 Vanishing gradient problem 때문에 뒤의 단어가 티켓이라는 것을 예측하기 어려울 것이다. 너무 멀리 떨어져 있기 때문이다.
그래서 gradient가 매우 작으므로 이 값에 곱해지는 learning rate를 크게 만드는 시도를 해보았다. 근데 수가 너무 증폭되어 NaN나 Inf가 나오는 경우도 발생해버린다. 그래서 gradient clipping도 해본다. gradient clipping이란 gradient 값이 너무 커지면 폭발하지 않도록 일정 비율을 곱해서 작게 만드는 것이다. 그런데 실제로 써보면 생각보다 도움이 되지 않는다고 한다.
그러면 이 vanishing gradient 문제를 어떻게 해결해야 할까? 메모리를 사용할 수는 없을까?
🔷 마치며, 흐름 정리
n-gram 모델의 단점(Sparsity, Storage Problem)을 해결해주기 위해 Neural LM이 등장했다. Neural LM은 워드 임베딩을 활용하여 Sparsity문제를, n-gram을 저장하지 않아도 되므로 Storage 문제를 해결했다. 하지만 이로부터 등장한 문제점은 input사이즈가 고정되어 있다는 것이고, symmetry하지 않다는 것이다. 그래서 RNN이 나왔다. RNN은 input사이즈가 고정되어 있지 않으며, 똑같은 W를 사용하기 때문에 symmetry하다. 동시에 순서를 고려할 수도 있다. hidden state에서 기억하고 있기 때문이다. 근데 RNN도 gradient vanishing이라는 문제점을 가지고 있었다. 다음 글에서는 이 문제를 해결하기 위한 LSTM에 대해 알아볼 것이다.
슬슬.. 이해를 다 못하고 넘어가는 부분이 생기기 시작하는ㄷ ㅔ......?
'자연어처리' 카테고리의 다른 글
| [자연어처리, CS224N] Lec8 : Self-Attention and Transformer (2) | 2024.04.30 |
|---|---|
| [자연어처리, CS224N] #6 - LSTM (1) | 2024.03.29 |
| [자연어처리 CS224N] #5-1. n-gram Language Model (1) | 2024.03.24 |
| [자연어처리 CS224N] #2-3. GloVe (2) | 2024.03.24 |
| [자연어처리 CS224N] #2-2. Skip-gram with Negative Sampling (1) | 2024.03.24 |