📍 퀵 정렬 (Quick Sort)
퀵 정렬은 빠르다고 해서 퀵 정렬이다. 먼저 퀵 소트의 기본 흐름은 아래와 같다.
1) 가장 왼쪽 원소를 pivot으로 선정 (pivot 선정 방식은 바꿀 수 있음)
2) 배열 내 원소들을 pivot보다 작은 것 / pivot보다 큰 것 이렇게 두 개로 분류
3) 각각의 배열 내에서 다시 1)부터 반복 (recursive)
📍 C++ 구현 코드
퀵소트를 구현하는 방식에는 Romuto의 방식, Hoare의 방식 두 개가 있다. 각 방식의 코드가 아래에 순서대로 있다.
// Romuto
class Solution {
public:
void quicksort(vector<int>& nums, int start, int end){
if(start<end){
int pivot = nums[start];
int i;
int j = start;
for(i=start+1;i<=end;i++){
if(nums[i]<pivot){
swap(nums[++j],nums[i]);
}
}
// pivot 자리 설정
swap(nums[j],nums[start]);
quicksort(nums, start, j-1);
quicksort(nums, j+1, end);
}
}
vector<int> sortArray(vector<int>& nums) {
quicksort(nums, 0, nums.size()-1);
return nums;
}
};// Hoare
class Solution {
public:
void quicksort(vector<int>& nums, int start, int end){
if(start<end){
int pivot = nums[start];
int i = start-1;
int j = end+1;
while(true){
while(pivot>nums[++i]);
while(pivot<nums[--j]);
if(i<j){
swap(nums[i],nums[j]);
}else{
break;
}
}
swap(nums[start],nums[j]);
quicksort(nums,start,j);
quicksort(nums,j+1,end);
}
}
vector<int> sortArray(vector<int>& nums) {
quicksort(nums,0,nums.size()-1);
return nums;
}
};https://leetcode.com/problems/sort-an-array/ 에서 위의 코드를 실행시킬 수 있습니다. (Romuto의 퀵 소트는 testcase는 통과하지만 시간초과 발생, Hoare의 퀵 소트는 정답으로 시간 내에 모든 케이스를 통과한다. 하지만 통과된 정답들 중에서는 매우 느린 편임을 확인할 수 있다.)
📍 코드 동작 원리
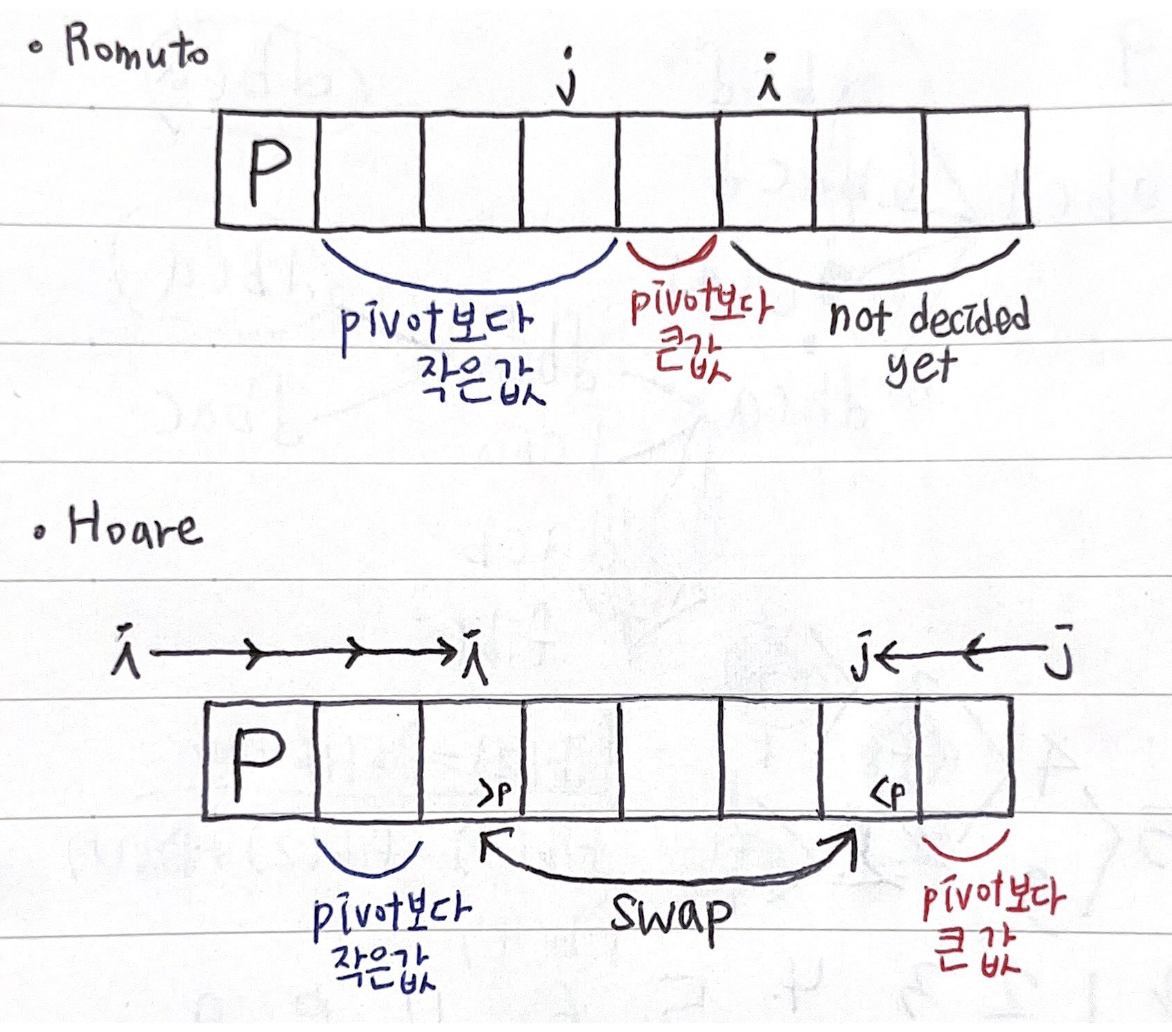
Romuto의 퀵 소트는 j 와 i 의 인덱스를 이용한다. pivot보다 작으면 j를 증가시키고 swap한다. pivot이 가장 왼쪽에 위치한 원소일 때 1부터 j까지는 pivot보다 작은 값, j+1부터 i까지는 pivot보다 큰 값, i부터 끝까지는 아직 결정되지 않은 값들이다.
Hoare의 퀵 소트는 왼쪽 끝에서부터 i를 증가시키다가 pivot보다 더 큰 값을 가진 원소에서 멈춘다. 오른쪽 끝에서부터는 j를 증가시키다가 pivot보다 더 작은 값을 가진 원소에서 멈춘다. i 인덱스의 원소와 j 인덱스의 원소를 swap한다. 그러면 1부터 i 인덱스 까지는 pivot보다 작은 값이 놓이게 되고, j부터 끝까지는 pivot보다 큰 값이 놓인다. i와 j 사이의 원소들은 아직 결정되지 않았다. i와 j의 인덱스가 역전되면(i가 j보다 커지면) 반복문을 종료한다.
1부터 j까지는 pivot보다 작은 값들만 모여 있지만 정렬은 되지 않은 상태이므로 이 배열에 대해서 재귀적으로 퀵 소트를 수행한다. (1부터 j까지인 이유는 반복문 종료 전에 인덱스 i와 인덱스 j와 교차되었기 때문이다. i가 j보다 더 큰 상태에서 더 이상 반복문의 조건이 만족하지 않아 반복문을 빠져나오게 된다.)
j+1부터 끝까지는 pivot보다 큰 값들만 모여 있지만 정렬은 되지 않은 상태이므로 이 배열에 대해서도 재귀적으로 퀵소트를 수행한다.
📍 시간복잡도(time complexity)
시간복잡도는 O(nlogn)이다. 아래 사진처럼 두 가지 방식으로 생각할 수 있다.

📍 Unstable / NOT In-Place
퀵소트는 Unstable한 정렬 알고리즘이다. swap이 많이 발생하기 때문인 것 같다. 또한 In-Place 알고리즘이 아니다. 추가적인 배열을 사용하지 않는 것처럼 보이지만 사실 재귀 호출로 인한 call stack 메모리 사용량 때문이다. 주어진 배열을 분할했을 때 균등하지 않게 분배되어 더 긴 배열과 짧은 배열이 생길 수 있다. 이때 짧은 배열을 먼저 처리한다면, 긴 배열의 길이만큼 재귀 호출 스택이 깊어진다. 이 최악의 경우 공간 복잡도는 O(n)까지 커진다. 즉 Not In-Place이다. 하지만 긴 배열을 먼저 처리하는 경우 (best case) 혹은 배열이 균등하게 나눠지는 경우(average case)에는 O(logn)이다.
배열이 정렬되는 양상을 시각적으로 떠올리면서 코드를 구현하는 것이 도움이 되는 것 같다. 그래서 자꾸 그림을 그려서 시각적으로 이해하고 기억하려고 노력했다.
'알고리즘' 카테고리의 다른 글
| [알고리즘] MST(Minimum Spanning Tree, 최소신장트리) - Kruskal, Prim 구현 (C++) (1) | 2024.11.25 |
|---|---|
| [알고리즘] 정렬알고리즘 #6 힙 정렬 (Heap Sort) (0) | 2024.10.23 |
| [알고리즘] 정렬알고리즘 #4 합병정렬 (Merge Sort) (0) | 2024.10.23 |
| [알고리즘] 정렬알고리즘 #3 버블정렬 (Bubble Sort) (1) | 2024.10.22 |
| [알고리즘] 정렬알고리즘 #2 선택정렬 (Selection Sort) (0) | 2024.10.22 |