하하 나는 인공지능을 많이 공부해보지 않아서 잘 모르는데... 어쩌다보니 자연어처리 수업을 듣게 됐다. 최대한 이해하려고 부여잡으면서 열심히 해볼게...
cs224n 강의자료를 활용하였고, 국민대학교 김장호 교수님의 강의를 듣고 정리한 글입니다.
공부하며 정리한 글이기에 오류가 매우매우 많을 수 있음을 밝힙니다.


우리는 단어를 어떻게 표현하는가?
단어에 대한 일반적인 언어의 사고방식은 denotational segmantics이다. 이는 '표의적(표시적) 의미론'이라고 한다.
우리는 '나무'라고 하면 자연스럽게 나무의 이미지가 떠오른다. 근데 컴퓨터는 어떻게 의미를 알지?

예전에 사용되던 방식은 WordNet 이었다. WordNet은 동의어(synonym sets)와 상의어(hypernyms)를 포함한 리스트이다. 아래 사진을 보자. good의 동의어와 panda의 상의어들이 저장되어 있는 것을 확인할 수 있다.
따라서 이러한 WordNet을 컴퓨터에 제공하면, 컴퓨터도 표의적 의미론으로서 단어의 의미에 접근할 수 있을 것이다.

따라서 WordNet은 유용한 자원이지만 많은 한계점을 가진다. 먼저 뉘앙스가 반영되지 못한다. 예를 들어 "proficient"라는 단어는 "good"의 동의어로 들어가 있지만, 모든 문맥에서 그렇지는 않다. 누군가 비꼬기 위해 이 단어를 사용했을 수도 있지 않은가. 두 번째로, 신조어가 생긴다는 점에서 한계를 가진다. 새로운 단어가 계속해서 생겨나지만 모든 단어를 매번 업데이트하기란 사실상 불가능하다. 또 단어를 넣어주는 과정을 사람이 번거롭게 작업해주어야 하며, 주관적일 수 있다. 마지막으로 단어의 유사도를 알 수 없다. WordNet에는 그냥 일일이 저장되어 있을 뿐, 단어들간의 유사도를 파악할 수는 없다.

단어들 간의 유사도를 알 수 없다는 것이 무슨 말인지 더 알아보자.
전통적인 NLP에서 단어를 표현할 때는 one-hot vectors를 사용했다. one-hot vectors란 단어를 벡터로 표현하는 방식으로, 표현하고 싶은 단어의 인덱스에만 1, 나머지는 모두 0으로 채워주는 것이다. 아래 사진에서 motel과 hotel 이라는 두 단어가 one-hot vectors의 방식으로 표현된 것을 확인할 수 있다. 하지만 직관적으로도 이 방식에는 문제점이 많아 보인다. 엄청나게 많은 단어를 표현하려면 벡터의 차원이 엄청나게 많이 필요할 것이다. 공간적으로 너무 낭비다. 또한 단어들 간의 유사도를 나타낼 수 없다. 예를 들어 motel과 hotel은 둘 다 숙박업소라는 점에서 유사도가 있지만, one-hot vectors로 표현된 방식으로는 이를 알 수가 없다.

벡터끼리 내적하면 유사도를 구할 수 있으므로 hotel과 motel 벡터 간의 유사도도 구할 수 있을 것이다. 코사인 유사도란 두 벡터 간의 코사인 각도를 이용하여 구할 수 있는 두 벡터의 유사도를 의미하는데, 벡터의 방향이 완전히 같으면 1, 90도의 각을 가지면 0, 완전히 다르면 -1의 값을 가진다. 결국 -1과 1사이의 유사도를 가지게 되는 것이다. 아래에 필기를 첨부하여 상기하기 쉽게 정리해보았다. (필기 수정: 세타 = 180 아래 ...을 더 넣어주는 것이 좋겠다)

자 다시 돌아와서, hotel과 motel 두 벡터 간의 코사인 유사도를 구하면 0이다. 이는 두 벡터 사이의 각이 90도를 이루고 있는 수직관계(orthogonal)임을 의미한다. 우리는 hotel과 motel 사이의 유사도가 높다고 나왔으면 좋겠는데 수직관계를 이루는 두 벡터의 유사도는 전혀 관계가 없다고 한다. 따라서 one-hot vectors로는 유사도를 나타낼 수 없다고 하는 것이다.

이를 해결할 수 있는 방법은 없을까?
you shall know a word by the company it keeps 라는 말이 있다. 우리는 문맥을 통해 단어의 의미를 알 수 있다. 따라서 이를 기반으로 학습 기반 임베딩에 대한 연구가 시작되었다. 임베딩이란 단어를 컴퓨터가 이해할 수 있게 표현해주는 방식이라고 생각하면 될 것 같다.

이렇게 문맥을 학습하여 임베딩된 결과를 보자. 아까는 one-hot vectors 방식으로 벡터 안에 0 혹은 1만 있었는데, 이제는 그렇지 않다. 아까의 표기 방식은 희소 표현(Sparse Representation) 방식이라고 하고, 이제는 그 반대인 밀집 표현(Dense Representation) 방식이라고 한다. 밀집 표현은 벡터의 차원을 단어 집합의 크기로 상정하지 않고 사용자가 설정한 값으로 모든 단어의 벡터 표현의 차원을 맞춘다. 그래서 더 이상 0과 1만이 아니라, 실수값을 가지게 된다.
banking(은행의)과 monetary(통화의, 돈의)의 벡터 방향이 유사해보인다. 이를 내적하여 코사인유사도를 구해보면 유사도가 꽤 높은 것으로 판단될 것 같다.
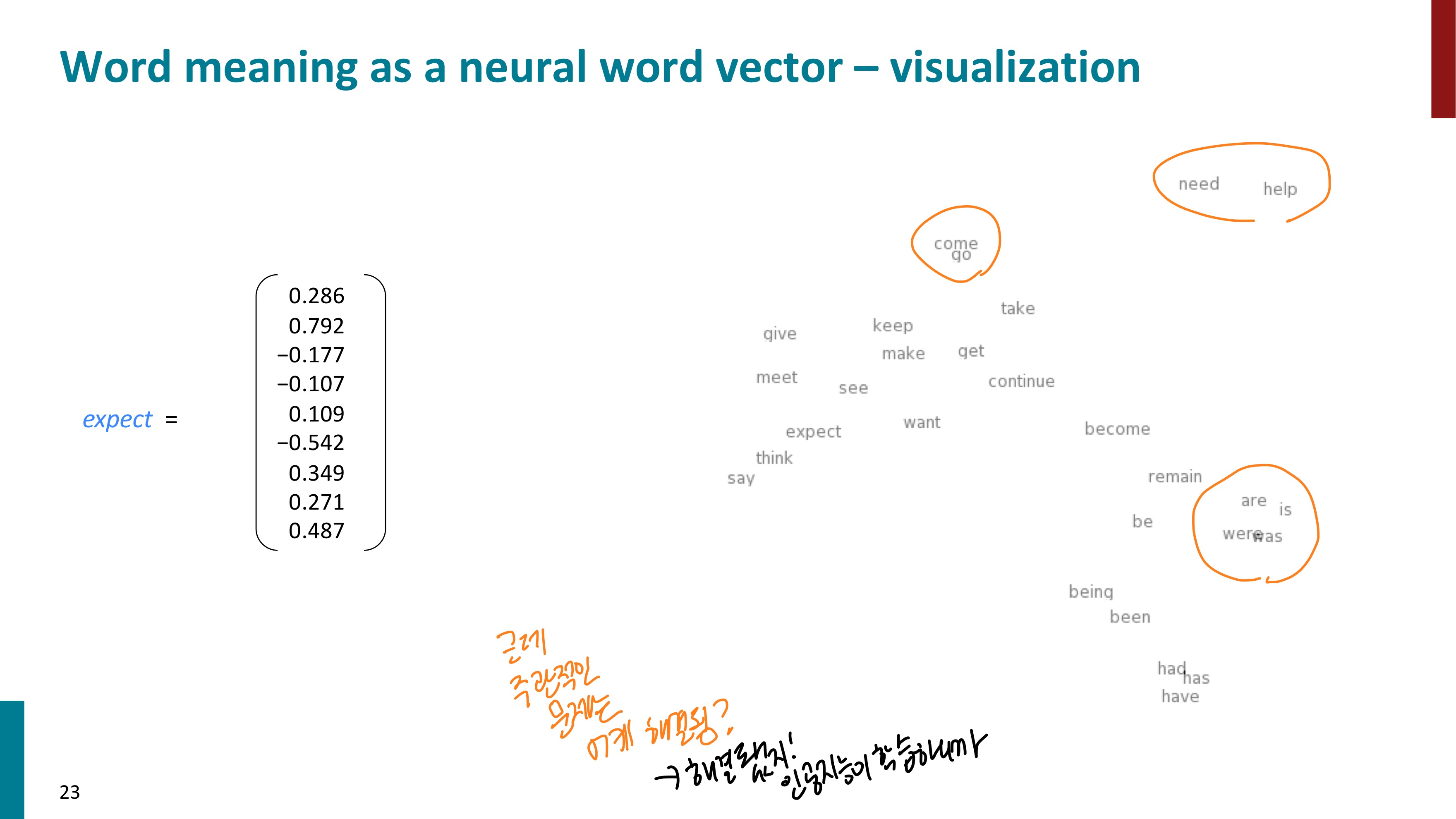
이러한 방식으로 학습한 단어들을 시각화하니 우리가 생각하는 단어의 의미와 맞게 유사도가 잘 표현되었음을 알 수 있다. 이러한 단어의 표현을 Word2vec이라고 한다. 단어를 벡터로 만든다는 뜻이다. 이는 단어 벡터 학습을 위한 프레임워크이다.

Word2vec은 학습 방식에 따라 두가지로 나뉘는데, CBOW와 Skip-gram 방식이 있다.
우리는 corpus라고 하는 말 뭉치들을 가진다. 이를 벡터로 표현할 것이다. 이 corpus에서 위치 인덱스를 t로 표현해보자. 위치 인덱스 t에 해당하는 위치의 단어를 center word라 하고 이를 c라고 표현하고, 그 주변 단어를 outside word, o라고 하자.

이미지를 보면 banking이라는 center word를 기준으로 양쪽의 단어 2개씩이 outside word가 되고 있다. 양쪽 2개씩인 이유는 window size를 2로 설정했기 때문이다. 중심 단어를 예측하기 위해서 앞, 뒤로 몇 개의 단어를 볼지를 결정했다면 이 범위를 윈도우(window)라고 한다. 그래서 P ( w(t+j) | w(t) ) 는 조건부 확률을 표기한 것이다. 말로 바꾸면 t의 위치에 있는 단어가 중심 단어일 때, t+j의 위치에 있는 단어가 나올 확률을 의미한다.
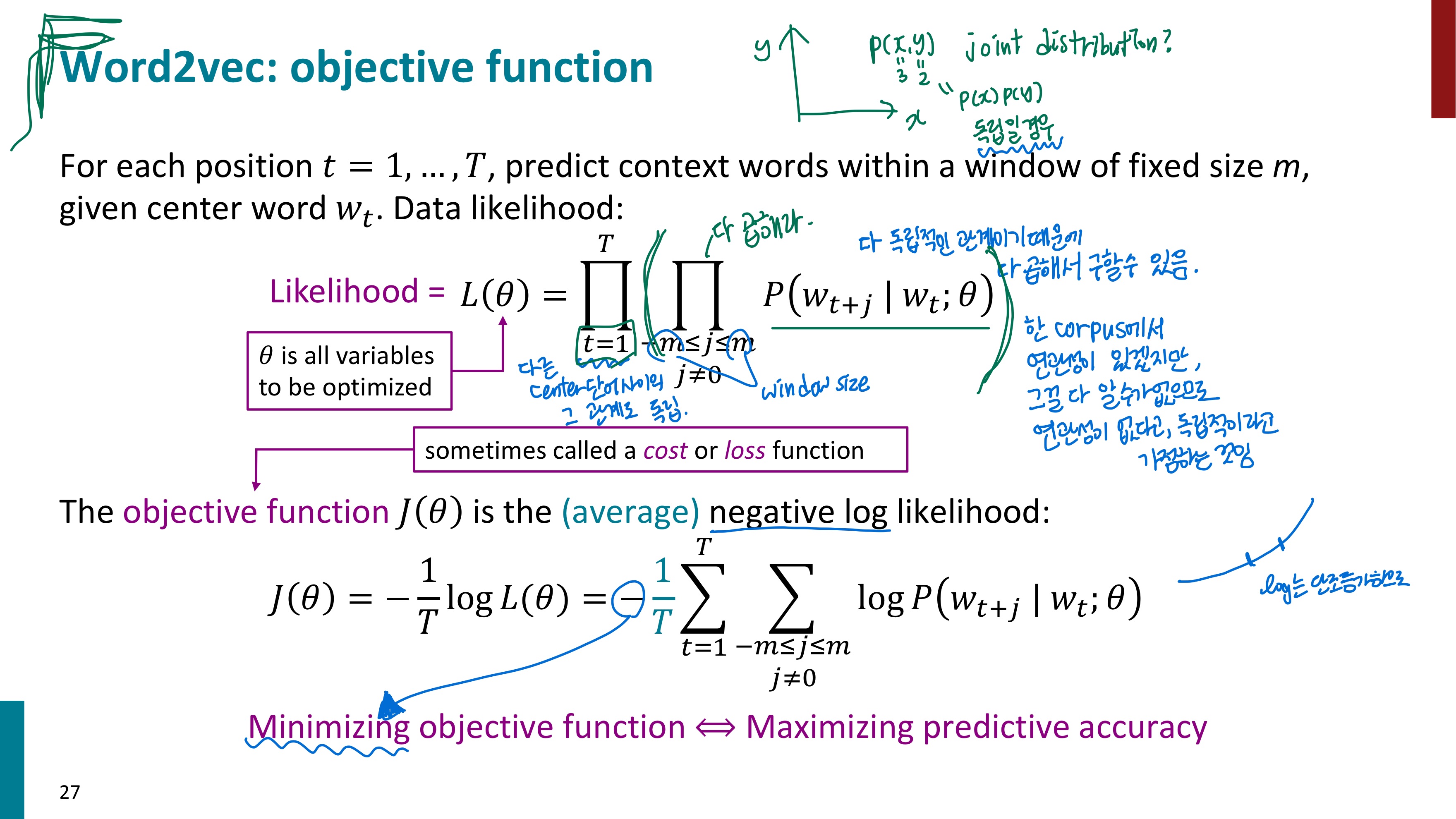
여기서부터 수식이 우르르 쏟아지는데... 차근차근 알아보자. 먼저 각 수식에서 나오는 여러 기호와 용어에 대해 설명하겠다. Word2vec를 이해하려고 하지 말고 먼저 식의 형태만 살펴보자.
1. 저 독립문처럼 생긴 기호는 파이이다. 시그마가 다 더하라는 의미라면 곱의 버전은 파이이다.
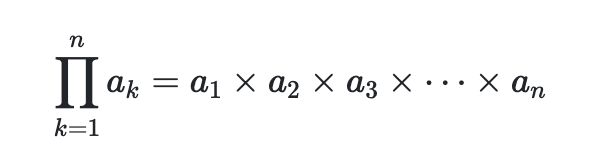
2. Likelihood = L(θ) 라고 되어 있는데, Likelihood란 한국어로 직역하면 가능도, 우도 라고 한다. 입력으로 주어진 확률 분포(파라미터)가 얼마나 데이터를 잘 설명하는지 나타내는 점수라고 한다. 이 함수에는 log를 씌워서 log-likelihood로 변경하는 경우가 많다. 이렇게 하는 이유는 덧셈 연산의 장점을 위해서이다. 여러 값들의 곱에 log를 씌우면 여러 값들의 합이 되므로 파이가 아닌 시그마를 통해 수식 표현이 가능해진다. (참고로 log 함수는 단조 증가하므로 그냥 막 붙여도 된다. log scale로 바뀌더라도 최댓값과 최솟값이 달라지지 않는다.) 결국 우리는 이 우도 함수가 가장 큰 값을 가지게 되는 파라미터 세타 θ 를 찾아야 한다.
3. 최적의 파라미터 세타 (θ)를 찾는 데에는 경사상승법(gradient ascent)를 이용할 수 있다. 우도 함수가 가장 큰 값을 가지도록 하는 추정방법이기 때문에 이를 MLE(Maximum Likelihood Estimation)이라고 한다. 그런데 대부분의 딥러닝은 경사하강법(gradient descent)를 지원한다. 그래서 object function이라고 쓰인 J(θ)를 보면 마이너스(-) 가 붙어 있다. 우도를 최대화하는 것이 아닌, 최소화하는 방법으로 최적의 파라미터를 구하고 싶어서 마이너스(-)를 붙여준 것이다. 이를 NLL(negative log-likelihood)라고 한다. Object function을 최소화하는 것이 예측정확도를 최대화하는 방향이다.
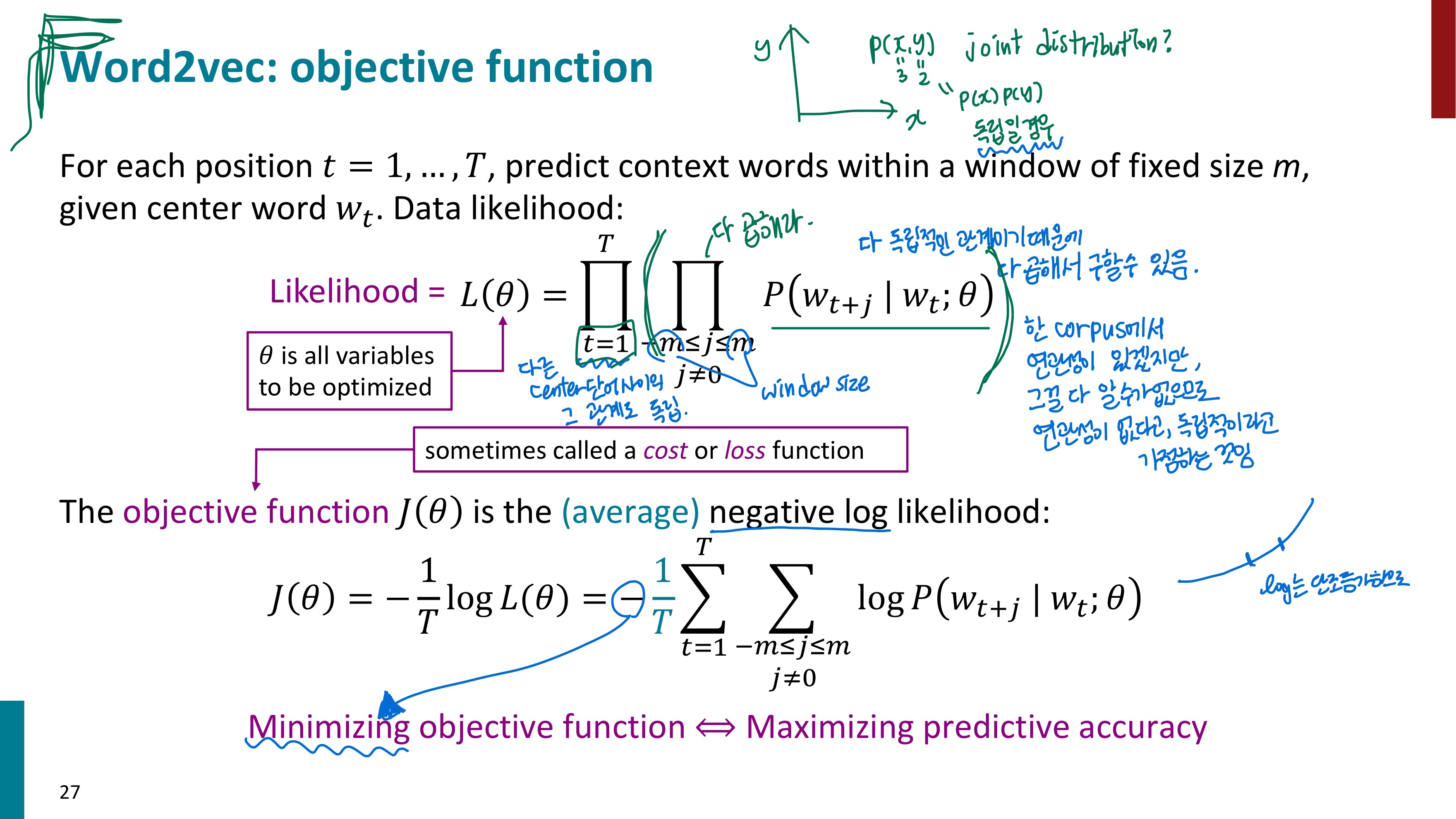
자 대충 수식의 형태와 용어들을 이해했으니, 이제 수식의 내용을 이해해보자. (편의를 위해 같은 이미지를 한번 더 첨부하였다.)
Likelihood 뒤로 파이 기호가 두 개 있고, 앞 슬라이드에서 보았던 조건부 확률이 보인다. P ( w(t+j) | w(t) )를 말로 바꾸면 t의 위치에 있는 단어가 중심 단어일 때, t+j의 위치에 있는 단어가 나올 확률을 의미한다. 그런데 그 앞에 있는 파이 기호가 있으므로 -m 부터 m까지(단 j는 0이 아님) 뒤 수식들을 모두 곱할 것이다. 이를 쭉 풀어 써보면 아래와 같다.
(t의 위치에 있는 단어가 중심 단어일 때, t-2의 위치에 있는 단어가 나올 확률) x (t의 위치에 있는 단어가 중심 단어일 때, t-1의 위치에 있는 단어가 나올 확률) x (t의 위치에 있는 단어가 중심 단어일 때, t+1의 위치에 있는 단어가 나올 확률) x (t의 위치에 있는 단어가 중심 단어일 때, t+2의 위치에 있는 단어가 나올 확률)
그런데 그 앞에 파이 기호가 하나 더 있다. 이 파이 기호는 t=1부터 t=T까지 뒤 값들을 전부 곱하라고 한다. 그러므로 이를 적당히 풀어 쓰면 아래와 같다.
[
{ (1 의 위치에 있는 단어가 중심 단어일 때, -1의 위치에 있는 단어가 나올 확률) x (1의 위치에 있는 단어가 중심 단어일 때, 0의 위치에 있는 단어가 나올 확률) x (1의 위치에 있는 단어가 중심 단어일 때, 2의 위치에 있는 단어가 나올 확률) x (1의 위치에 있는 단어가 중심 단어일 때, 3의 위치에 있는 단어가 나올 확률) } x
{ (2 의 위치에 있는 단어가 중심 단어일 때, 0의 위치에 있는 단어가 나올 확률) x (2의 위치에 있는 단어가 중심 단어일 때, 1의 위치에 있는 단어가 나올 확률) x (2의 위치에 있는 단어가 중심 단어일 때, 3의 위치에 있는 단어가 나올 확률) x (2의 위치에 있는 단어가 중심 단어일 때, 4의 위치에 있는 단어가 나올 확률) } x
...
{ (T 의 위치에 있는 단어가 중심 단어일 때, T-2의 위치에 있는 단어가 나올 확률) x (T의 위치에 있는 단어가 중심 단어일 때, T-1의 위치에 있는 단어가 나올 확률) x (T의 위치에 있는 단어가 중심 단어일 때, T+1의 위치에 있는 단어가 나올 확률) x (T의 위치에 있는 단어가 중심 단어일 때, T+2의 위치에 있는 단어가 나올 확률) }
]
이 값이 Likelihood가 된다. 여기서 짚고 넘어가야 하는 것은 이 확률들간의 관계이다. 확률을 다 곱할 수 있었던 것은 이 확률들이 서로 독립적인 관계이기 때문이다. 이렇게 확률 변수가 두 개 이상일 때 여러 사건이 동시에 일어날 확률을 결합 분포(Joint Distribution)이라고 한다. 그런데 왜 독립 관계지?라는 의문이 들 수 있다. 문장 내에 단어들 사이에는 당연히 연관성이 있을 것이기 때문이다. 하지만 이는 무시하고 연관성이 없다고, 독립적이라고 가정한다. 이 연관성을 다 알고 표현할 방법이 없기 때문이다.
앞에서 살펴보았기 때문에 object function도 이해할 수 있을 것이다. 여기서 object function은 average negative log likelihood 이다.
average를 구하기 위해 1/T를 앞에 곱했고, negative 이기 때문에 마이너스가 붙었다. 시그마 기호로 바꿔주기 위해 log도 붙였다.


object function을 최소화하기 위해서는 조건부 확률을 수식적으로 나타낼 수 있어야 한다. 이를 위해 우리는 단어 하나 당 두 가지 벡터를 사용한다. v는 단어가 중심 단어일 때의 벡터이고, u는 단어가 주변 단어일 때의 벡터이다. 이제 저 수식이 관건인데.. 우선 저 형태는 Softmax 함수이다. softmax 함수부터 알아보고 수식을 이해해보자.
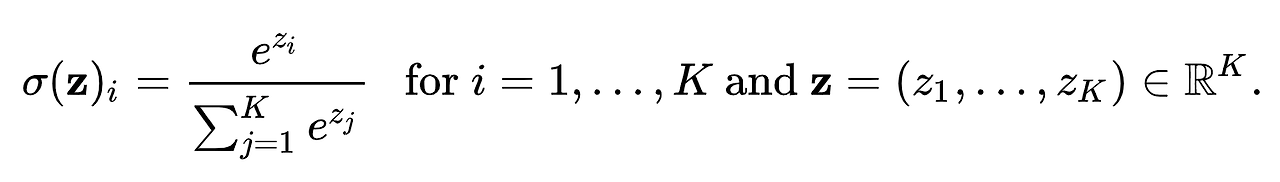
Softmax 함수란 분류 작업을 위해 신경망에서 널리 사용되는 함수라고 한다. 이 함수는 임의의 실수 벡터를 확률 분포로 변환하며 벡터의 각 요소는 특정 클래스의 확률을 나타내게 된다. 소프트맥스 함수의 형태는 위와 같다. 입력 벡터의 각 구성 요소를 지수화한 다음 지수화된 각 값을 지수화된 모든 값의 합으로 나눈다. 이렇게 하면 모든 확률의 합이 1이 되어 함수의 출력이 유효한 확률 분포가 된다. Softmax 함수는 큰 값을 지수화하여 더 큰 값으로 만들어주면서(max) 작은 값은 여전히 작게 유지하기 때문에(soft) Softmax라는 이름을 가지고 있다.
자 그럼 다시 수식을 보자. 분자에 있는 것은 "중심 단어의 v 벡터와 주변 단어의 u 벡터의 내적"을 지수화한 값이다. 두 벡터를 내적하면 뒤에 오는 벡터를 전치시킨 후 행렬곱하는 것과 같은 식이 되므로 저렇게 "주변 단어의 u 벡터의 전치와 중심 단어의 v벡터의 곱"으로 표현되었다. 분모에는 "중심 단어의 v벡터와 주변 단어의 w 벡터의 내적"이 지수화된 값인데, 모든 단어에 대해서 주변 단어일 때를 다 더했다. 잘 이해가 가지 않을 것이니 예를 들어보자.

"I am a good zebra" 라는 말이 있다고 해보자. 각 단어에 해당하는 v와 u벡터를 숫자와 알파벳으로 간단히 표기했다. 위 필기의 수식을 이해할 수 있을 것이다.
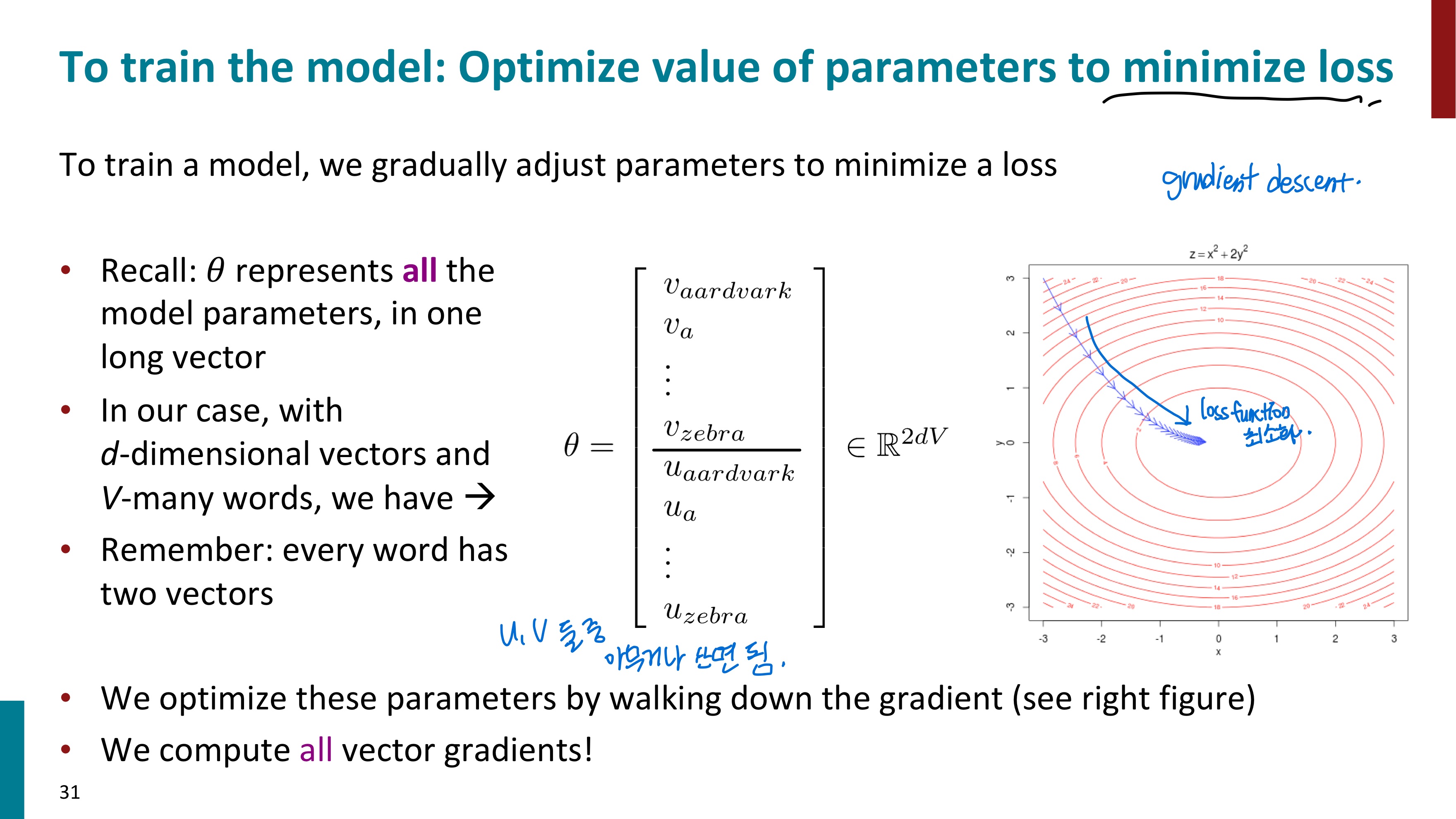
이러한 방식으로 조건부 확률 값을 구할 수 있다. 그럼 거의 다 왔다. 이제 모델을 학습시키면서 손실을 최소화하는 최적의 파라미터 값을 찾아내면 된다. 경사하강법(gradient descent)를 통해 이 과정을 수행한다. 최적의 파라미터를 찾은 후에는 이제 학습된 벡터값들을 가져다가 사용하면 된다. 단어마다 v와 u 두 가지 벡터를 가질텐데 둘 중에 무엇을 사용하느냐는 상관이 없다. 성능에 큰 영향을 미치지 않는다고 한다.
경사하강법에 대해 잠시 알아보고 넘어가자. 경사하강법이란 미분계수를 통해 함수의 최솟값을 찾아가는 방법이다. 경사하강법은 함수의 기울기를 이용하여 x의 값을 어디로 옮길지를 결정한다. 만약 기울기가 양수라면 x 값이 작아지는 음의 방향으로 이동해야 함수 값도 작아질 것이다. 만약 기울기가 음수라면 x 값이 커지는 양의 방향으로 이동해야 함수 값도 작아질 것이다.
( xi+1=xi−이동 거리×기울기의 부호 ) x를 얼마나 옮길 지에 대한 x의 이동거리는 gradient값과 step size를 곱한 값으로 사용한다.
그러면 진짜 마지막으로 함수를 직접 미분해보자. ... 첫 번째 이미지는 내가 다시 쓰면서 풀어본 내용으로, 그 아래 4개의 이미지와 같은 내용을 담고 있다.



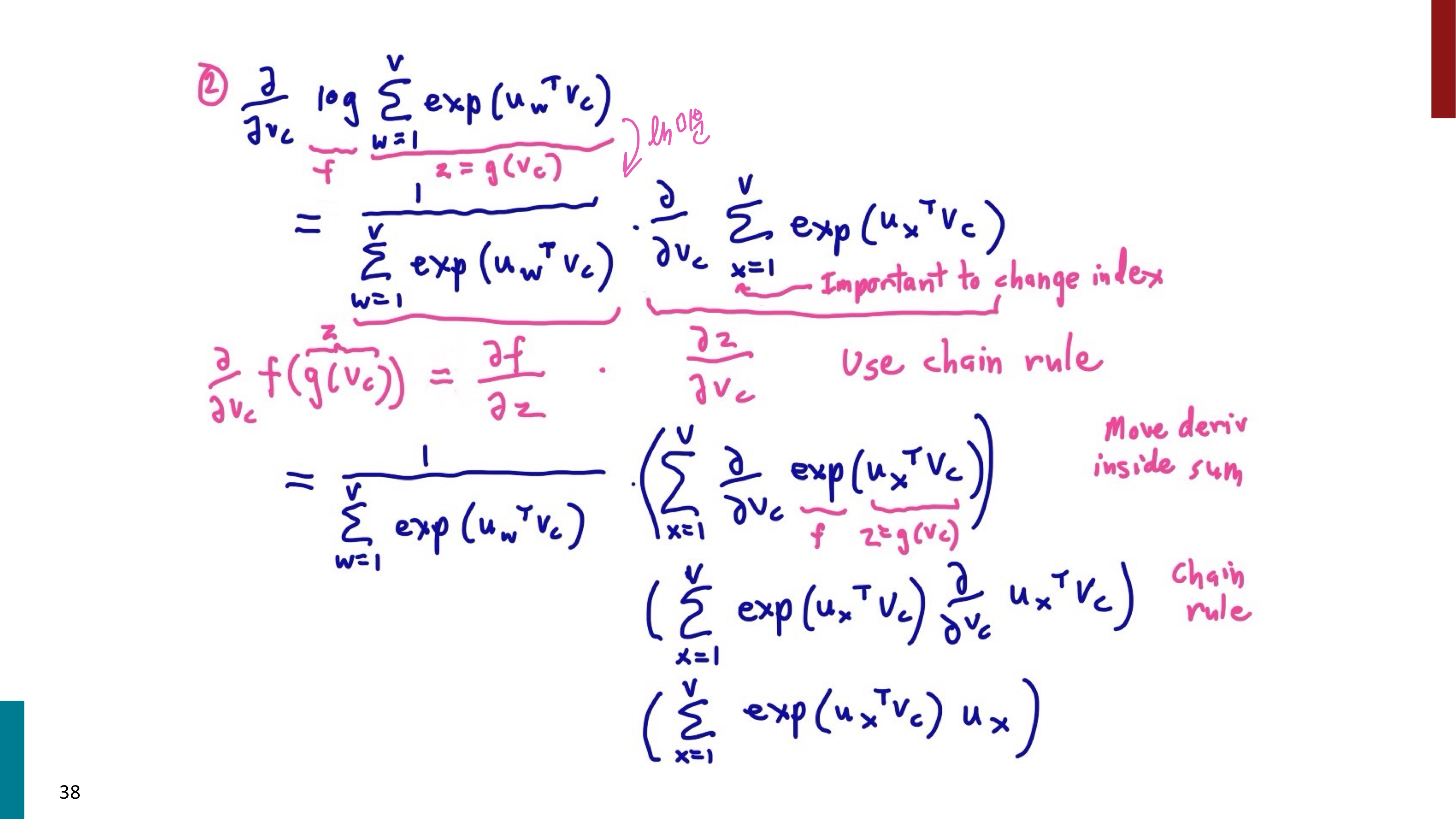

'자연어처리' 카테고리의 다른 글
| [자연어처리 CS224N] #5-2 Neural Language Model, Perplexity (0) | 2024.03.26 |
|---|---|
| [자연어처리 CS224N] #5-1. n-gram Language Model (1) | 2024.03.24 |
| [자연어처리 CS224N] #2-3. GloVe (2) | 2024.03.24 |
| [자연어처리 CS224N] #2-2. Skip-gram with Negative Sampling (1) | 2024.03.24 |
| [자연어처리 CS224N] #2-1. Word2Vec Optimization (SGD) (1) | 2024.03.19 |